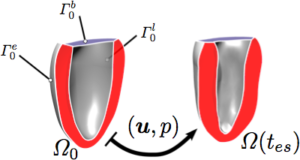
In publication in Lecture Notes in Computer Science (contact L. Asner for Pre-print).
The STACOM cardiac modeling challenge was an effort hosted by Alistair Young, Martyn Nash, and Vicky Wang of the University of Auckland Bioengineering Institute as part of the MICCAI conference in Boston 2014. Completed by 8 cardiac modeling groups around the world, the challenge asked participants to predict the left ventricular function of four canine hearts. Participants were provided with:
- Masks (or point clouds) of the geometry at end diastole, end systole and diastasis
- Pressure / Volume loops for each dog
- 1 Anatomical Image per dog
- Fibre data
 CHeart Approach
CHeart Approach
Simulations were run in CHeart using a novel Energy minimization approach with a series of new boundary condition types to better approximate behavior in the truncated left ventricle. These included:
- new volume boundary conditions preserving volume estimates with base plane motion
- new energy minimizing basal conditions minimizing applied forces due to data uncertainty
- new image potential-based boundary conditions to incorporate exterior conditions
Importantly, the results were run using volume loading conditions using Lagrange multipliers. Data assimilation through systole and diastole relied then on the pressure observations provided, enabling model parameter tuning using Reduced Order Unscented Kalman Filtering developed by Dominique Chapelle and colleagues at inRIA.
While convergence was obtained, we proved the parameterization problem was non-unique, producing multiple minima which could reconstruct the PV loop data (see left). Focusing simply on diastole, we sampled the parameter space of the model examining the behavior of our objective function (L2 pressure error in space-time). From this, we clearly see that multiple pressure observations are insufficient for parameterizing the reduced Holzapfel-Ogden law. This added inherent uncertainty to the model results which would require further data to ensure adequate material parameterization.
Model parameters were then selected and whole-cycle simulations ran for each dog geometry. Convergence tests (4 levels of uniform refinement) were run for all dogs to ensure displacement and stress measures were accurate. The largest variations (approximately ~5%) between middle and fine grid simulations were observed in the stress, with displacement errors significantly lower.
CHeart Challenge Results
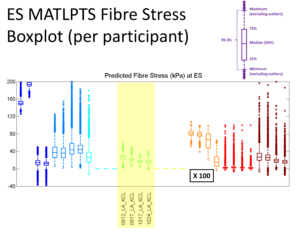
Organizers compared displacements and fiber stress results between groups. While ground truth data was available for displacements, stresses were reported for comparative purposes. Displacements between groups showed similar performance overall, with CHeart results performing strongly in these predictions. However, fiber stress better elucidated differences between groups, showing a wide range of values in most group results. More homogeneity in the CHeart results stemmed from applied boundary conditions which minimized stress peaks. Moreover, median values of these results are of the same order as first order approximations by Laplace Law (for a thick walled ellipsoid).